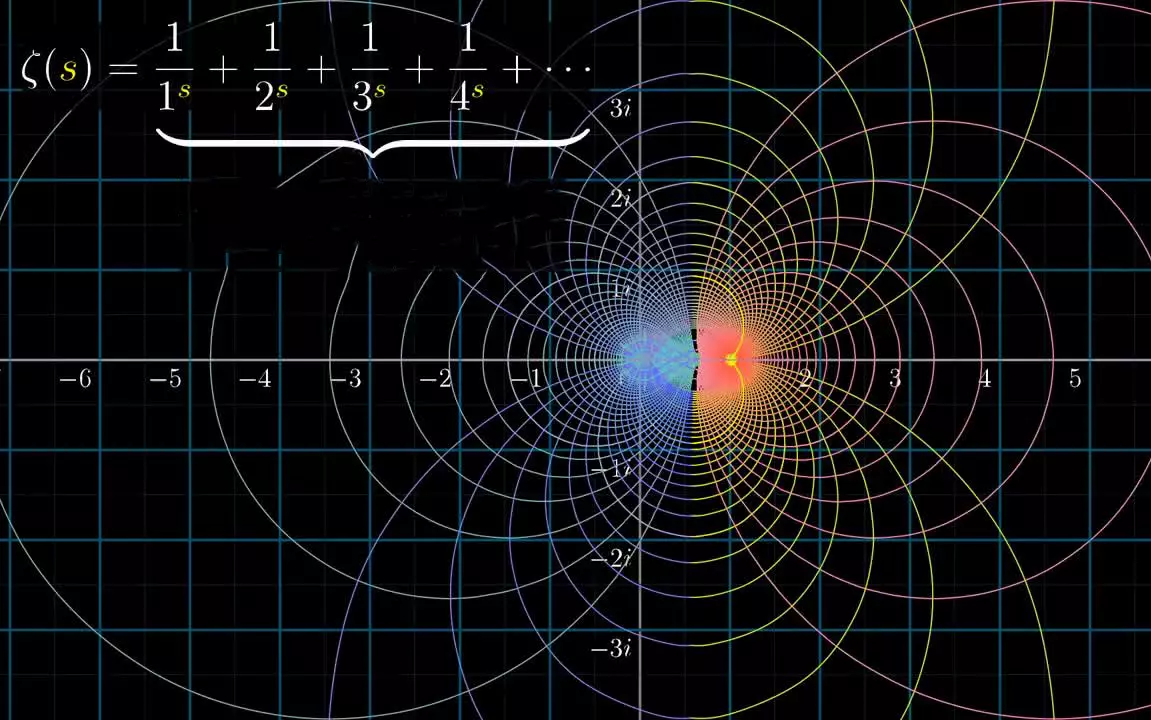
Мир математики изобилует задачами, чья сложность и значимость вызывают восхищение и уважение. Одной из таких задач является Гипотеза Римана – предположение, связанное с распределением простых чисел, оставшееся одним из самых нерешенных математических вопросов на протяжении почти двух веков. Гипотеза Римана, предложенная Бернхардом Риманом в 1859 году, утверждает, что все нетривиальные нули дзета-функции Римана имеют действительную часть, равную 1/2. До настоящего времени не была найдена проверка гипотезы, способная утверждать, что гипотеза Римана верна, или, напротив, обнаружено опровержение гипотезы, указывающее на то, что гипотеза Римана неверна.
Исторический контекст: Жизнь и работа Бернхарда Римана
Бернхард Риман, имя которого носит знаменитая гипотеза, был одним из самых влиятельных математиков XIX века. Его работы затрагивали несколько областей математики, включая анализ, геометрию и теорию чисел. Главным образом, такой интерес вызван исследованием дзета-функции Римана, определенной для комплексных чисел. Значение этой функции и ее нули являются ключевыми в формулировке гипотезы Римана, основы которой заложены именно в его работах. Проливающая свет на природу простых чисел, гипотеза Римана уже давно стала краеугольным камнем теоретической математики.
Основы Гипотезы Римана и ее влияние на математику
Основной постулат Гипотезы Римана касается свойства нулей дзета-функции Римана. Дзета-функция, ζ(s), где s — комплексное число, имеет бесконечное количество нулей, и именно распределение этих нулей, согласно Риману, подчиняется определенному порядку. Если бы была доказана гипотеза, это существенно продвинуло бы наше понимание простых чисел.
Существует два основных типа нулей дзета-функции Римана:
- Тривиальные нули, которые находятся на отрицательной вещественной оси и равны отрицательным четным числам.
- Нетривиальные нули, расположенные в критической полосе комплексной плоскости.
Истинность гипотезы означала бы, что все нетривиальные нули имеют действительную часть, равную 1/2, что приведет к более глубокому пониманию распределения простых чисел.
Попытки доказательства и знаковые достижения
Многие выдающиеся математики предпринимали попытки доказательства гипотезы, при этом ее истинность не была опровергнута. На сегодняшний день некоторые заслуги в исследовании гипотезы были достигнуты, но окончательное доказательство все еще не представлено.
| Год | Математик | Достижение |
|---|---|---|
| 1914 | Годфри Харди | Доказал бесконечность количества нулей на прямой 1/2 |
| 1942 | Атле Сельберг | Работа над явными формулами, связанными с нулями |
| 1974 | Хью Монтгомери | Сформулировал парные корреляции нулей |
| 1980-е | Эндрю Одлызко | Вычисления, подтверждающие гипотезу для первых нулей |
Гипотеза Римана и ее связь с другими математическими проблемами
Гипотеза Римана, предложенная Бернхардом Риманом в 1859 году, является одной из самых знаменитых и долгоживущих нерешенных проблем в теории чисел и математике в целом. Она утверждает, что все нетривиальные нули дзета-функции Римана имеют действительную часть, равную 1/2. Связь этой гипотезы с другими математическими проблемами многочисленна и глубока:
- Распределение простых чисел: Гипотеза Римана имеет непосредственное отношение к пониманию распределения простых чисел, что влияет на многие области математики и криптографии.
- Квантовая механика: Интересные параллели между нулями дзета-функции Римана и спектрами некоторых операторов в квантовой механике были обнаружены, что способствует развитию обеих областей.
- Теория чисел: Многие гипотезы и теоремы в теории чисел, включая закон взаимности и теоремы о простых числах, тесно связаны с гипотезой Римана, предполагая глубину её влияния на фундаментальные аспекты математики.
- Статистика и случайные процессы: Существуют связи между статистическими свойствами нулей дзета-функции и теорией случайных матриц, что открывает новые пути для исследований в области математической физики и за её пределами.
Сложности и вызовы в понимании гипотезы
Понимание и доказательство гипотезы Римана сталкивается с рядом сложностей и вызовов, делающих её одной из самых загадочных проблем в математике. В первую очередь, гипотеза затрагивает глубокие аспекты аналитической теории чисел, требуя разработки новых математических инструментов и подходов. Среди проблем:
- Высокая абстрактность: Дзета-функция Римана и её нули оперируют в области комплексных чисел, что добавляет уровень абстракции и сложности в анализ и визуализацию.
- Недостаток интуитивно понятных подходов: Многие попытки доказательства гипотезы требуют сложных аналитических и численных методов, зачастую выходящих за рамки интуитивного понимания.
- Связь с другими математическими теориями: Гипотеза Римана пересекается с множеством других областей математики, что требует широкого спектра знаний и понимания этих связей для её анализа.
- Технические трудности: Даже с современными методами компьютерного моделирования, точная проверка нулей дзета-функции на соответствие гипотезе Римана представляет собой огромную вычислительную задачу.
- Отсутствие единой стратегии доказательства: Несмотря на множество предпринимаемых попыток, до сих пор не существует универсального метода или стратегии, которая позволила бы доказать гипотезу Римана или полностью понять её последствия.
Влияние на смежные области науки и технологий
Гипотеза Римана оказывает глубокое влияние на смежные области науки и технологий, выходя далеко за пределы теории чисел. В криптографии, например, понимание распределения простых чисел, к которому приводит гипотеза, имеет критическое значение для безопасности шифрования и цифровых подписей. В области квантовой физики, аналогии между нулями дзета-функции и спектрами квантовых систем открывают новые пути для понимания квантового хаоса и статистической механики. В математической физике, связь с теорией случайных матриц помогает в изучении сложных систем, от ядерной физики до нанотехнологий. Таким образом, гипотеза Римана остаётся не только одной из величайших загадок математики, но и ключевым элементом, связывающим различные дисциплины, открывая перед ними новые горизонты исследований.
Заключение: Почему Гипотеза Римана остается актуальной
Гипотеза Римана остаётся актуальной и привлекает внимание учёных по множеству причин. Во-первых, она занимает центральное место в теории чисел, связывая воедино множество математических концепций и предполагая глубокое понимание природы простых чисел. Во-вторых, её потенциальное доказательство или опровержение способно радикально изменить наше понимание математики и открыть новые направления исследований в смежных областях, включая криптографию, квантовую физику и компьютерные науки. Кроме того, загадочность и вызов, который она представляет, мотивируют развитие новых математических методов и технологий. Таким образом, гипотеза Римана не только остаётся одной из ключевых нерешённых проблем математики, но и продолжает быть маяком, направляющим научное сообщество к новым открытиям и разработкам на стыке дисциплин.
Часто задаваемые вопросы
- Что такое дзета-функция Римана? Дзета-функция Римана – это комплексная функция, важная для понимания распределения простых чисел.
- Почему Гипотеза Римана считается одной из главных проблем в математике? Она удерживает ключ к пониманию фундаментальных свойств чисел и их распределения.
- Каковы основные подходы к доказательству Гипотезы Римана? Исследователи используют инструменты теории чисел, комплексного анализа, а также комбинаторики и алгебраической геометрии.
- Если Гипотеза Римана будет доказана, как это повлияет на другие науки? Решение окажет значимое влияние на несколько областей, от криптографии до физики высоких энергий.
- Каковы достижения в исследовании Гипотезы Римана в последние годы? Прогресс включает компьютерное значение множества нулей и теоретическое развитие новых подходов к анализу.